A relação entre dois conjuntos é o que determina uma função, na qual um desses conjuntos depende de outro, ou seja, está em função de outro. Para representarmos a relação entre essas duas variáveis podemos usar os seguintes métodos:
Método das setas
O método das setas, também conhecido como diagrama das flechas, trabalha com dois conjuntos numéricos, o Domínio e o Contradomínio. Dentro do contradomínio encontramos um subconjunto chamado Imagem. A Imagem é o subconjunto dos elementos dentro do contradomínio que recebem setas, ou seja, aqueles elementos que possuem alguma relação com o conjunto Domínio. Veja um exemplo abaixo:
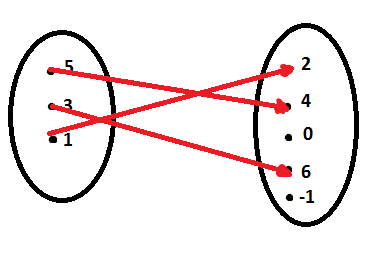
O domínio, que também pode ser chamado de x da função, corresponde ao primeiro diagrama oval. O conjunto numérico que envia as setas sempre é o domínio. Para representar o conjunto dos elementos do domínio da função temos que: D(f) = {5, 3, 1}.
O outro diagrama oval corresponde ao contradomínio e logo podemos perceber que nem todos os seus elementos recebem setas do Domínio. Para representar o conjunto dos elementos do contradomínio da função temos que: CD(f) = {2, 4, 0, 6, -1}.
Já a imagem é o conjunto dos elementos dentro do contradomínio que receberam setas do domínio. A imagem representa, também, o y da função. Para representar o conjunto dos elementos da imagem da função temos que: Im(f) = {2, 4, 6}.
Condição de existência
Todos os elementos do domínio devem possuir um correspondente no contradomínio, caso ao contrário, o que foi representado no diagrama não é uma função.
Um mesmo domínio não pode possuir duas imagens, ou seja, duas setas não podem sair de um mesmo elemento no domínio.
Tipos de funções
1) Função Sobrejetora: Uma função é sobrejetora quando todos os elementos do contradomínio fazem parte da imagem, ou seja, quando todos os elementos recebem uma seta do domínio.

2) Função Injetora: Nessa situação, cada elemento do contradomínio deve possuir uma única e distinta imagem. Além disso, na função injetora podem existir elementos do contradomínio que não fazem parte da imagem.

3) Função Bijetora: Uma função é dita bijetora quando é sobrejetora e injetora ao mesmo tempo, ou seja, quando todos os elementos do contradomínio fazem parte da imagem e recebem apenas uma seta do domínio.

4) Função Simples: É quando a função não é Injetora nem Sobrejetora. Ou seja, quando nem todos os elementos do contradomínio recebem seta e os elementos que compõem a imagem recebem mais de uma seta.

