Duas circunferências que possuem o mesmo centro são chamadas de concêntricas e, nesses casos, podem vir a possuir raios diferentes. A coroa circular é justamente uma região delimitada por dois círculos concêntricos com raios diferentes.
No exemplo abaixo, percebemos que as duas circunferências compartilham o mesmo centro, mas possuem raios diferentes. Como é perceptível, R é maior do que r, sendo a coroa circular a região proveniente da diferença do maior raio e do menor.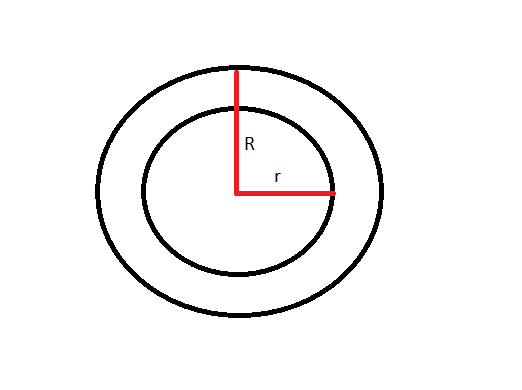
A área de uma coroa circular também pode ser calculada através da diferença entre a área da maior circunferência e da menor.
- Área da coroa = Área do maior círculo – Área do menor círculo
- Área da coroa = πR2 – πr2
- Área da coroa = π(R – r)2
Exemplos
1) Determine a área de uma coroa circular formada por duas circunferências de raio 6 cm e 3cm.
- Área da coroa = π62 – π32
- Área da coroa = 36π - 9π
- Área da coroa = 27π cm2
2) Uma coroa circular possui 95 π cm2 de área e o raio da menor circunferência concêntrica que a forma é 7cm. Descubra o valor do raio da maior circunferência.
- Área da coroa = πR2 – πr2
- 95 π = πR2 – π72
- 95π = πR2 - 49π
- 95π + 49π = πR2
- 144π = π R2
- R2 = 144
- R = √ 144
- R = 12
O maior vale 12 centímetros.
Exercícios resolvidos
1) Um fazendeiro resolveu marcar seus tratores pintando os pneus, apenas pelo lado de fora, com uma tinta vermelha. Sabendo que o metro quadrado de tinta custa R$ 1,20, que o fazendeiro pintou 4 pneus e que a parte pintada de cada pneu representa uma coroa circular com raio menor igual a 1 metro e o raio maior igual a 1,5 metros, quanto esse fazendeiro gastou com tinta? Considere π = 3,1
Conhecendo os raios, podemos encontrar a área da coroa circular.
- Área da coroa circular = π(1,52 – 12)
- Área da coroa circular = π(2,25 – 1)
- Área da coroa circular = 3,1 (1,25)
- Área da coroa circular = 3,875 m2
- Se cada roda possui 3,875 m2 de coroa e cada metro quadrado de tinta custa R$1,20:
- 3,875*1,20 = 4,65
- 4,65 * 4 = 18,60
Uma vez que 4 pneus foram pintados, o fazendeiro gastou R$18,60.
2) (PM ES – CFO – Exatus 2013). Adriana planta flores num canteiro circular de raio 8 m. Ao redor desse canteiro, ela pretende plantar ervas medicinais formando uma coroa circular, de maneira que a parte destinada às flores sofrerá uma redução de 2 m em seu diâmetro. A área ocupada pelas ervas medicinais neste canteiro será igual a:
a) 13π
b) 14π
c) 15π
d) 16π
e) 8π
Sabendo que o diâmetro é duas vezes o raio, percebemos que o canteiro de flores terá 1 metro de raio a menos, ou seja, terá 7 metros de raio e o de plantas medicinais 8 metros de raio.
Sendo assim, a área ocupada pelas ervas medicinais é exatamente a área da coroa circular formada pelas duas circunferências.
- Área da coroa circular = π(R2 – r2)
- Área da coroa circular = π(82 – 72)
- Área da coroa circular = π(64 – 49)
- Área da coroa circular = 15π, letra c.

