John Venn criou, através de análises lógicas, um método de diagramação que consiste simploriamente em uma relação entre círculos capaz de demonstrar operações entre conjuntos numéricos.
O Diagrama de Venn é um método que, através do desenho de figuras planas, os círculos, é utilizado para resolver questões de conjuntos numéricos.
Por outro lado, existe também a fórmula (A U B) = n(A) + n(B) - n(A ∩ B) que nos permite realizar a união de três elementos.
Através do diagrama, as operações dos conjuntos são representadas nos círculos e suas interações. No diagrama abaixo, são representados três conjuntos.
Os espaços em azul representam as intersecções entre dois conjuntos de cada vez e o espaço central em vermelho a intersecção entre todos os três conjuntos.

Representação de um único conjunto
Conjunto P dos números pares menores do que 12, P = {2, 4, 6, 8, 10}
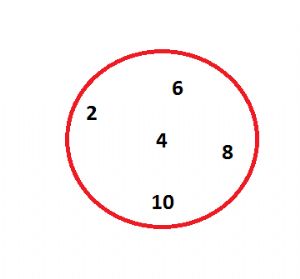
Representação de dois conjuntos
Conjuntos A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} e B = {1, 3, 5, 7, 9, 11, 13, 15}.

Nesses dois conjuntos temos que A U B (união) = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 13, 15} e que A ∩ B (intersecção) = {1, 3, 5, 7, 9}.
Representação de três conjuntos
Dados os conjuntos A = {2, 4, 6, 8, 10, 12}, B = {3, 6, 9, 12} e C = {4, 8, 12, 16}.

Nesses conjuntos temos que A ∩ B = {6}, A ∩ C = {4, 8}, B ∩ C = {Ø} e A ∩ B ∩ C = {12}.
Exercícios resolvidos utilizando o diagrama de Venn
Veja os exemplos abaixo:
1) Em uma sala de aula, a professora de Matemática decidiu fazer um levantamento dos lanches comprados pelos alunos. A professora verificou que, de um total de 35 alunos, dezesseis compraram salgado; destes, quatro compraram pizza e salgado, e sete alunos não compraram lanche nesse dia. Quantos alunos compraram apenas pizza?
Resolução:
Em um primeiro momento, precisamos identificar que na questão existem dois conjuntos: o conjunto dos alunos que compraram salgado e o conjunto dos alunos que compraram pizza.
Em segundo lugar, precisamos considerar que no universo dos 35 alunos existem 7 que não compraram lanche e, sendo assim, não estarão inclusos nos círculos dos conjuntos.
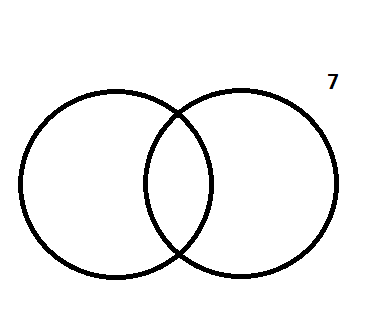
Agora devemos incluir os números cedidos aos seus lugares correspondentes no nos círculos. Porém, devemos sempre começar pela intersecção entre todos os conjuntos sendo ela o valor correspondente aos alunos que compraram tanto a pizza quanto o salgado. Veja:

Após isso, utilizaremos a informação dos dezesseis alunos que compraram salgado. Se inserirmos o valor cedido no espaço correspondente aos salgados, teremos um diagrama errado. Veja o porquê:
Se 16 alunos compraram salgado, estamos considerando também os 4 alunos que além do salgado compraram também a pizza.
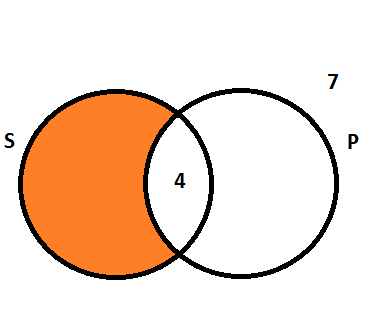
O espaço em laranja corresponde aos alunos que compraram apenas os alunos que compraram o salgado, sem incluir aqueles que também compraram pizza. Justamente por isso não podemos incluir o número 16 diretamente no espaço em laranja, mas sim subtrair 16 do número de alunos que compraram os dois lanches para encontrar aqueles que compraram apenas o salgado.
n(A - B) = n(A) - n(A ∩ B)
16 – 4 = 12
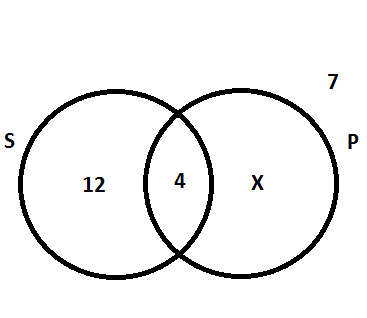
Agora, a incógnita X representa a informação pedida pela questão, ou seja, os alunos que só compraram pizza.
Se ao total temos 35 alunos, 7 nada compraram, 12 compraram apenas salgado e 4 pizza e salgado, se relacionarmos esses elementos ao X em uma igualdade poderemos encontrar o valor da incógnita.
35 = 12 + 4 + 7 + X
35 = 23 + X
X = 12
Ou seja, 12 alunos compraram apenas pizza.
2) Numa pesquisa, verificou-se que, das pessoas consultadas, 100 se informavam pelo site A; 150 por meio do site B; 20 buscavam se informar por meio dos dois sites, A e B; e 110 não se informavam por nenhum desses dois sites. Desse modo, é correto afirmar que o número de pessoas consultadas nessa pesquisa foi de?
Resolução:
Sabemos que o conjunto A possui 100 pessoas o B possui 150 e a intersecção entre A e B equivale a 20 pessoas. Podemos retirar do enunciado, também, que 110 pessoas fazem parte da pesquisa, mas não fazem parte do conjunto A ou B, mas mesmo assim pertencem ao conjunto universo.
Como ensinado anteriormente, sempre começamos pela intersecção entre todos os conjuntos, veja abaixo:
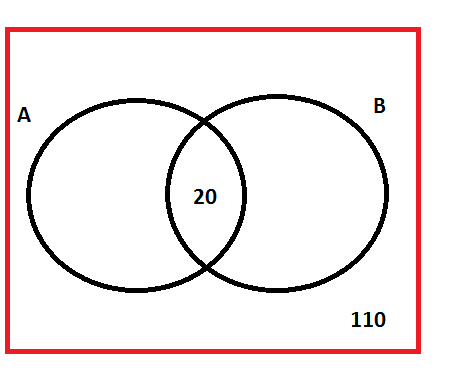
Se 100 pessoas fazem parte do conjunto A e já temos 20 pessoas dentro do círculo correspondente a A, nos restam 80 pessoas para completar o total. Agora, o conjunto B possui 150 pessoas no total, entretanto devemos contabilizar as 20 pessoas que pertence à intersecção entre A e B, ou seja, as que informaram A e B. Sendo assim, 150 – 20 = 130. Desse modo obtemos o número de pessoas que informaram apenas o site B.

Se a questão pede o total de pessoas consultadas, precisamos apenas somar todos os elementos presentes no diagrama.
80 + 20 + 130 + 110 = 340
Ou seja, foram entrevistadas 340 pessoas.
3) Uma sorveteria, com o intuito de otimizar suas vendas, fez uma pesquisa para saber qual era o sorvete que seus clientes mais consomem. Entre os entrevistados, 130 consomem o sorvete de morango; 165 consomem o sorvete de chocolate e 175 consomem o sorvete de flocos. Dentro desse grupo, 120 consomem apenas sorvete de flocos; 25 consomem sorvete de morango e chocolate; 15 consomem o sorvete de morango e flocos; 10 consomem sorvete de morango, flocos e de chocolate. Quantos clientes consomem os sorvetes de chocolate e flocos?
Resolução:
Começaremos pelos clientes que consomem os 3 sabores de sorvete, ou seja, a intersecção entre os três conjuntos.
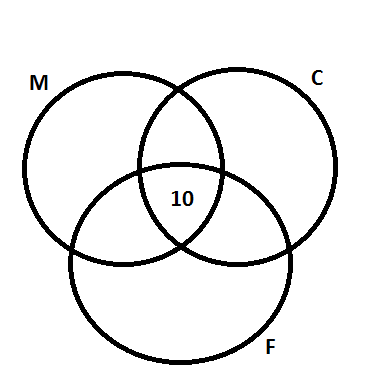
Sabemos que a questão pede o valor da intersecção entre os sorvetes de chocolate e flocos, é preciso colocar uma incógnita no espaço correspondente no diagrama de Venn. Além disso, podemos preencher os espaços cujos valores foram informados no enunciado.

Se o total de consumidores do sorvete de flocos é 175, podemos relacionar todos os elementos do conjunto F com a incógnita através de uma igualdade resultará na resposta pedida pela questão.
175 = 15 + 10 + 120 + X
175 = 145 + X
X = 30
Ou seja, 30 clientes consomem o sorvete de chocolate e de flocos.


